The behavior of superconductors suggests that electron pairs are coupling over a range of hundreds of nanometers, three orders of magnitude larger than the lattice spacing. Called Cooper pairs, these coupled electrons can take the character of a boson and condense into the ground state.

A visual model of the Cooper pair attraction has a passing electron which attracts the lattice, causing a slight ripple toward its path. Another electron passing in the opposite direction is attracted to that displacement. This constitutes a coupling between electrons which can be depicted in a Feynman diagram.

As strange as such an interaction seems, it is experimentally supported by the isotope effect and the evidence for a condensation to a boson -like state at the critical temperature for superconductivity.

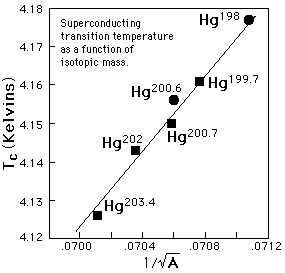
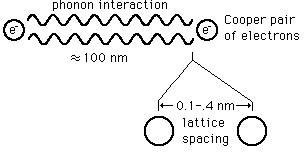
If electrical conduction in mercury were purely electronic, there should be no dependence upon the nuclear masses. This dependence of the critical temperature for superconductivity upon isotopic mass was the first direct evidence for interaction between the electrons and the lattice. This supported the BCS theory of lattice coupling of electron pairs.

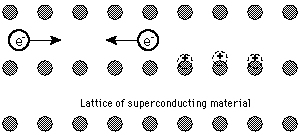
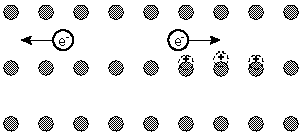
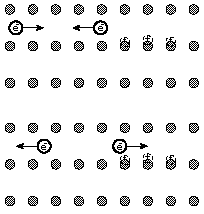
It is quite remarkable that an electrical phenomenon like the transition to zero resistivity should involve a purely mechanical property of the lattice. Since a change in the critical temperature involves a change in the energy environment associated with the superconducting transition, this suggests that part of the energy is being used to move the atoms of the lattice since the energy depends upon the mass of the lattice. This indicates that lattice vibrations are a part of the superconducting process. This was an important clue in the process of developing the BCS theory because it suggested lattice coupling, and in the quantum treatment suggested that phonons were involved.